Elementy (księgi tej nie należy mylić z późniejszymi, a dużo bardziej znanymi Elementami Euklidesa) - opisują główne dokonania pitagorejczyków w zakresie geometrii.
Hipokrates z Chios (nie należy mylić go z Hipokratesem z Kos - patronem lekarzy - w medycynie przysięga Hipokratesa i czepiec Hipokratesa pochodzą właśnie od tego drugiego) był utalentowanym geometrą i członkiem Związku Pitagorejskiego, z którego został jednak wyrzucony za nauczanie geometrii za opłatą. Jest dziś uważany za Judasza wśród pitagorejczyków, gdyż to jemu przypisuje się wyjawienie (w odwecie za usunięcie z ruchu) tajemnicy istnienia odcinków bez długości (czyli o długości niewymiernej), która doprowadziła do rozłamu wśród pitagorejczyków (niektóre źródła przypisują ten czyn innemu pitagorejczykowi - Hippiaszowi z Metapontu). Nawet jeśli pobudki Hipokratesa nie były szlachetne, po raz pierwszy w historii osiągnięcie naukowe zostało ogłoszone publicznie, a nie przekazane kręgowi wtajemniczonych naukowców.
Hipokrates z Chios swoje dorosłe życie rozpoczął od zajmowania się handlem morskim. Gdy podczas jednej z podróży poborcy z Bizancjum ograbili go ze wszystkich pieniędzy, doszczętnie zrujnowany, zajął się matematyką. Wstąpił do szkoły pitagorejskiej i został matematykiem. Działał w Atenach ok. 450-420 p.n.e. Był twórcą systemu aksjomatycznego geometrii, który nie zachował się do dziś, zajmował się problemami delijskimi.
Dowód a contrario 
Hipokrates z Chios wymyślił rozumowanie "przez sprowadzenie do sprzeczności" (tzw. dowód apagogiczny, nie wprost, a contrario). Rozumowanie takie opiera się na zasadzie kontrapozycji implikacji prostej, czyli oparte jest na tautologii:
a → b jest równoważne ¬ b → ¬ a,
co pozwala ustalić prawdziwość twierdzenia, dowodząc, że z zaprzeczenia jego tezy wynika sprzeczność z założeniami. Odmianą tego typu rozumowania jest dowód "przez sprowadzenie do niedorzeczności" (do absurdu), w którym z zaprzeczenia tezy wynika sprzeczność z wcześniej udowodnionymi twierdzeniami lub przyjętymi aksjomatami.
Podwójna średnia proporcjonalna
Hipokrates z Chios sprowadził problem podwojenie sześcianu (tzn. zadanie skonstruowania za pomocą cyrkla i linijki bez podziałki krawędzi sześcianu o objętości dwukrotnie większej od danego sześcianu ? był to jeden z problemów delijskich) do znalezienia podwójnej średniej proporcjonalnej. Nowa (x) i stara (y) długość krawędzi powinny spełniać zależność: a/x = x/y = y/2a, gdzie a jest dane. Dopiero w XIX wieku niemożliwość wykonania takiej konstrukcji wykazał Pierre Laurent Wantzel.
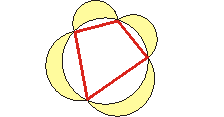
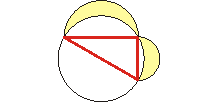
Księżyce Hipokratesa
Z dzieł Hipokratesa zachował się do czasów nowożytnych tylko fragment o tzw. księżycach Hipokratesa wielokąta wpisanego w okrąg. Są to figury wycięte z płaszczyzny przez łuki półokręgów, których średnicami są boki tego wielokąta oraz przez okrąg na nim opisany. Hipokrates zauważył, że dla trójkąta prostokątnego suma pól księżyców Hipokratesa równa jest polu tego trójkąta (dlaczego?). Zauważmy, że dzięki tej obserwacji można łatwo skonstruować kwadrat o polu równym polu księżyców Hipokratesa trójkąta prostokątnego, a zatem dokonać ich kwadratury. Była to pierwsza w historii kwadratura figury krzywoliniowej.
 |
|
- Hipokrates z Chios do Związku Pitagorejskiego trafił jako kompletnie zdruzgotany finansowo handlarz.
- Został z niego wyrzucony za nauczanie geometrii za pieniądze.
- W odwecie zdradził odkrycie, że długość przekątnej kwadratu jednostkowego nie wyraża się żadną liczbą (Grecy znali wówczas tylko liczby wymierne).
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
