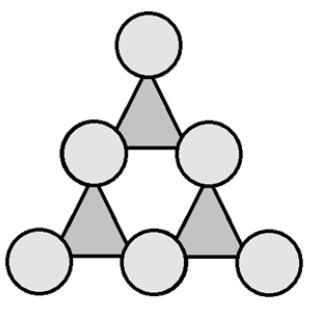
Zad. 1. W kółka wpisz rózne liczby od 1 do 6, tak aby suma liczb w wierzchołkach każdego małego trójkąta była liczbą pierwszą. W odpowiedzi podaj liczby wierszami, oddzielając wiersze przecinkiem.
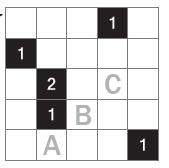
Zad. 2. Ustaw żarówki tak, aby każde białe pole diagramu było oświetlone. Żarówka oświetla wszystkie pola znajdujące się w tym samym wierszu i kolumnie co ona, aż do pola zaczernionego. czarne pola blokują dostęp światła. Żadna żarówka nie może oświetlać innej żarówki. Liczby w diagramie oznaczają, ile żarówek znajduję się na polach przylegających bokiem do pola z liczbą. W odpowiedzi podaj tylko zawartość pól A, B, C: wpisz 1, jeśli w danym polu znajduje się żarówka, i 0 w przeciwnym razie.
Zad. 3. Pewna kobieta ma troje dzieci, a połowa z nich to chłopcy. Jak to możliwe?
Za rozwiązania zadań listopadowych punkty zdobyli:
- 3 pkt. - Andrzej Piasecki - administrator IT z Oleśnicy,
- 2 pkt. - Krystyna Lisiowska - redaktor z Warszawy, Piotr Mazur - urzędnik ze Złotoryi,
- 2,5 pkt. - Agata Jeziorna ZSP Lubań, Małgorzata Konarska - nauczycielka matematyki z Ostrzeszowa, Anna Magierewicz ZSP Lubań, Marzena Wąsiewicz - gospodyni domowa z Kajetan,
- 1,5 pkt. - Miłosz Cichuta GM 1 Wrocław, Kosma Kasprzak XXXVIII LO Poznań, Pataki Moneg ???, Radosław Przekop ???,
- 0,5 pkt. - Daria Bumażnik - studentka chemii i toksykologii sądowej na UWr.
Po dwóch miesiącach w czołówce Ligi są:
- 6 pkt. Andrzej Piasecki
- 5,5 pkt. - Małgorzata Konarska, Marzena Wąsiewicz
- 5 pkt. - Piotr Mazur, Krystyna Lisiowska.
Zad. 1. Są dwa rozwiązania prowadzące do sum 7, 13, 13 lub 11, 11, 11. Przykładowe układy liczb pokazano na rysunku (inne powstają z nich przez symetrie osiowe i obroty). Za podanie jednego rozwiązania przyznawano 0,5 pkt.
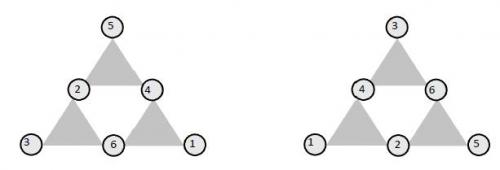
Zad. 2. W polach A, B, C powinny stać: 1, 0, 0.

Zad. 3. Kobieta ma samych synów.



 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.


