Czy z jednej siatki można skleić dwa różne wielościany? Oczywiście że tak. Pewne części tej siatki możemy bowiem skleić "na wypukło" lub "na wklęsło". Na przykład z siatki z poniższego diagramu można skleić oba modele przedstawione na poniższych rysunkach.
Klikając w powyższy diagram, można pobrać siatkę w formacie pdf. Szarym kolorem zostały zaznaczone "skrzydełka" ułatwiające sklejanie bryły. Można je pominąć przy wycinaniu, jeżeli bryła ma być klejona po wierzchu taśmą klejącą.
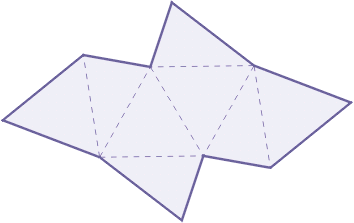
A czy można z jednej siatki utworzyć dwa różne wielościany wypukłe? Nie jest to już tak oczywiste, ale okazuje się możliwe. Wytnij siatkę z poniższego rysunku i spróbuj złożyć z niej dwa różne wielościany.
Klikając w powyższy diagram, pobierzesz siatkę w formacie pdf.
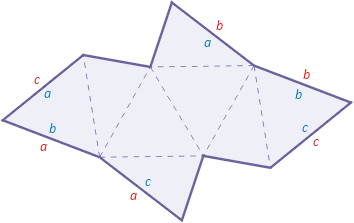
Na poniższym rysunku krawędzie sklejane w pierwszym modelu podpisano kolorem czerwonym, a te sklejane w drugim modelu - kolorem niebieskim. W zależności od tego, które krawędzie siatki skleimy, otrzymamy różne bryły. W pierwszym przypadku będzie to dwupiramida prostokątna, a w drugim - połowa pewnej dwupiramidy sześciokątnej o nieforemnej podstawie.
Otrzymane bryły przedstawiają poniższe zdjęcia.
Okazuje się, że w przypadku wielościanów wypukłych, z jednej siatki z podpisanymi krawędziami, które mają być sklejane, można już złożyć wielościan w sposób jednoznaczny. Mówi o tym twierdzenie Cauchy'ego [czytaj: kosziego] o sztywności wielościanów wypukłych, udowodnione w 1813 roku przez francuskiego matematyka Augustina Louisa Cauchy'ego. W swoim dowodzie popełnił on jednak błąd, ponieważ nie rozważył wszystkich przypadków. Pomyłka ta pozostała niezauważona przez ponad 50 lat, jednak później dowód uzupełniono.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
