MAT-ŚWIAT › Odlotowe figury

Wianuszki

Data ostatniej modyfikacji:
2015-07-23
Autor: 
Krzysztof Omiljanowski
pracownik IM UWr
Poziom edukacyjny: 
szkoła średnia z maturą
szkoła profilowana zawodowa
Dział matematyki: 
geometria syntetyczna
Rysunki utworzono z pomocą programu MSWLogo.


 

U6,5
Obok widać, jak we wnętrzu n-kąta foremnego rosną na jego bokach m-kąty foremne. Rosną tak długo, aż 'chwycą się za ręce', tzn. rosną dopóki ich wnętrza nie mają punktów wspólnych. Wianuszkiem n,m nazwiemy ów finalny układ wielokątów.
 
Najtrudniejsza w wykonaniu takich rysunków jest nie tyle symulacja ruchu, lecz obliczenie, kiedy ten ruch ma się zakończyć.
 
Sedno sprawy tkwi w znalezieniu zależności pomiędzy długością a boku dużego n-kąta foremnego, a długością x boków małych m-kątów foremnych tworzących wianuszek.

Badaliśmy już wianuszki, w których n, m były liczbami 3, 4, 6 (zajrzyj koniecznie do artykułu Wianuszki - rozgrzewka).

 

 

Nawet dla niezbyt dużych wartości m (na rysunkach poniżej m = 18) wianuszki wyglądają jak zbudowane z okręgów.

U3,18

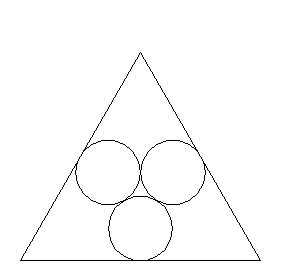
Zadanie A. Wyznacz promienie y okręgów tworzących wianuszek w n-kącie foremnym o boku a, gdy

    3)    n = 3,

    4)    n = 4,

    6)    n = 6,

    n)    n = n (dla dowolnego n).

Wskazówka.

Zatem dla dużych wartości m mamy
                                        x     y   =   a . tg(45o-90o/n) .
Można oszacować błąd tego przybliżenia:
        a . tg(45o-90o/n) . 2 sin(180o/m)     x     a . tg(45o-90o/n) . 2 tg(180o/m) .
 

 

 

Dla dużych wartości n (na rysunkach poniżej n = 36) zewnętrzny n-kąt wygląda jak okrąg o obwodzie n . a.

U36,3
Dla m = 3 mamy x = a .

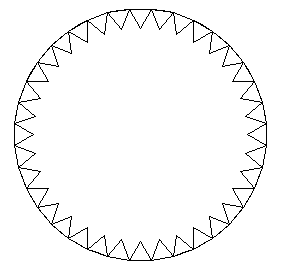
Dla m = 4 widać, że w przybliżeniu
            nx + 2x    na   (dlaczego?).
Stąd
            x    a / (1 + 2/n).
(Czy to jest przybliżenie z góry, czy z dołu?)

Podobnie dla m = 6 widać, że w przybliżeniu
            2x    a ,
czyli
            x    a / 2 .

 
Te obserwacje nie są uniwersalne i dają tylko wartości przybliżone.

 

 

Wydaje się, że ogólnie, dla wianuszka Un,m do wyznaczenia x jako funkcji zmiennej a potrzeba jedynie żmudnej trygonometrii. Nie tylko!
Kluczową sprawą jest rozstrzygnięcie, którymi wierzchołkami stykają się m-kąty w wianuszku.

rysunki:
Dla U5,9 widać, że są to trzecie wierzchołki, licząc od boków dużego wielokąta, k=3.
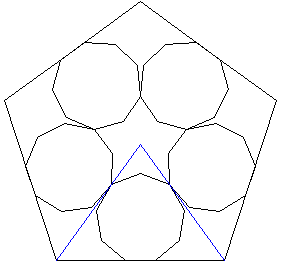
Jaka własność pozwoli obliczyć (a nie tylko zobaczyć na rysunku), że są to trzecie wierzchołki?

Rysunki 1 - 5 obok wyjaśniają ten problem.
Wędrujemy po obwodzie m-kąta (w wierzchołkach skręcamy o 360o/m) aż dojdziemy do wierzchołka sąsiedniego m-kąta, czyli:
- zaznaczone czerwone kąty są wielokrotnościami 360o/m ,
- zaznaczone czerwone kąty są nie większe od różowego (rys. 5).

Zatem szukamy największej liczby naturalnej k takiej, że

k . 360o/m    90o + 180o/n .
Po podzieleniu przez 360o/m widać, że
szukamy największej liczby naturalnej k takiej, że
k    m/4 + m/n/2 .
Dzięki pojęciu funkcji część całkowita, powyższe zdanie zapiszemy jako równość
 
(*)     w Un,m m-kąty stykają się k-tymi wierzchołkami, gdzie   k  =  [ m/4 + m/n/2 ] .
 

Dalej już nie ma zmiłuj. Pozostaje do wykonania żmudne rachunki trygonometryczne.

Przypomnijmy, że szukamy uniwersalnej zależności pomiędzy x i a, czyli między długościami boków wielokątów w wianuszku Un,m. (Ilustracja poniżej pozwoli wyznaczyć te ogólne zależności.) Przyjmujemy, że k jest określone jak wyżej.
 

          

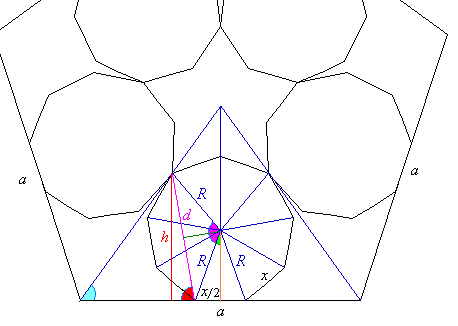
Oto szkic rozumowania.

(1)   Wyznaczamy miary zaznaczonych kątów:
          -   niebieski ma   180o/n  i  AEB = 180o/n ,
          -   zielony ma   180o/m ,
          -   różowy ma   k . 360o/m ,
          -   żółty ma   90o - k . 180o/m   (dlaczego?),
          -   czerwony ma   (k+1) . 180o/m   (dlaczego?).

(2)   Wyznaczamy długości odcinków R, d, b w zależności od x i powyższych kątów. W efekcie dostajemy b zależne tylko od x, n, m, k .
          b   =   d . sin BCE   =
               =   2R sin(k/m.180o) . sin((k+1)/m.180o)  =
               =   x / sin(180o/m) . sin(k/m.180o) . sin((k+1)/m.180o)  .

(3)   Dalej jest żmudnie.

a/2   =   AB + BC + x/2 ,
a/2   =   b sin AEB + b ctg BCE + x/2 ,
a/2   =   b sin(180o/n) + b ctg((k+1)/m.180o) + x/2 ,
a   =   b . 2( sin(180o/n) + ctg((k+1)/m.180o) ) + x .

(4)   Dalej, po wstawieniu b z (2) do (3), pozostaje (tylko?!) żmudne wyliczenie x

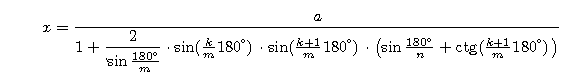
(5)   Na koniec należy jeszcze w powyższym wzorze wpisać  [ m/4 + m/n/2 ]  w miejsce k.

 

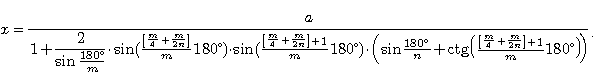
Powyższy wzór nie wydaje się 'ładny'. Ale mimo to opisuje 'ładne' wianuszki. Jest to język opisu wianuszków potrzebny na przykład do tego, by komputer kreślił automatycznie takie obrazki.
Jest to pewna reklama trygonometrii. Koduje zależności, dzięki którym łatwiej opisać i wianuszki, i ruch planet, i drgania strun, i wiele innych zjawisk.

 

 

Zadanie B. Dla jakich liczb n, m w wianuszkach Un,m wewnętrzne m-kąty stykają się krawędziami?

 

 

V6,5
Obok widać przykłady wianuszków innego rodzaju. Tutaj małe wielokąty, rosnąc na bokach dużego wielokąta, 'stoją' a nie 'leżą' na nich. Oznaczmy taką kolekcję wianuszków symbolem Vn,m.
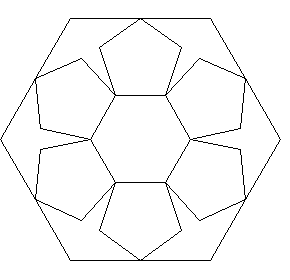
Teoria kolekcji Vn,m tylko nieznacznie różni się od teori przedstawionej powyżej dla kolekcji Un,m.

PROBLEM C. Znajdź zależność pomiędzy x i a, długościami boków wielokątów foremnych w wianuszkach typu Vn,m.

 

 

Nietrudno wyobrazić sobie m-kąty foremne rosnące na bokach n-kąta foremnego, ale nie do wewnątrz, jak to rozważaliśmy powyżej, lecz na zewnątrz. Oznaczmy takie kolekcje symbolami Uzn,m oraz Vzn,m.

PROBLEM D. Znajdź zależność pomiędzy x i a, długościami boków wielokątów foremnych w wianuszkach typu Uzn,m.

PROBLEM E. Znajdź zależność pomiędzy x i a, długościami boków wielokątów foremnych w wianuszkach typu Vzn,m.

 

 

O przestrzennych wianuszkach możesz przeczytać w artykule Wianuszki 3D.

 

 

Powrót na górę strony