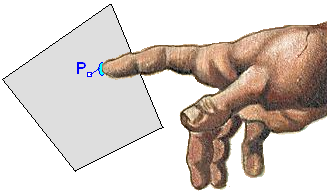
Gdy pinezką P przyszpilimy figurę wyciętą z kartonu, chwilę się pokołysze i znieruchomieje.
W jakim położeniu?
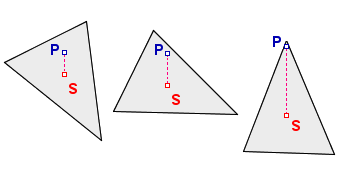
Fizyka mówi: to zależy od położenia środka ciężkości.
Ale co to jest środek ciężkości (figury płaskiej)?
Czy to jest taki punkt S, że:
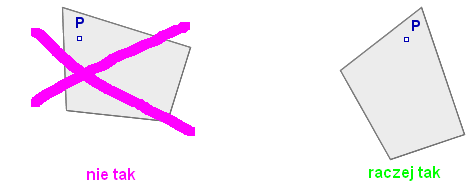
- gdy jakkolwiek przypniemy figurę,
punkt S znajdzie się pod pinezką?
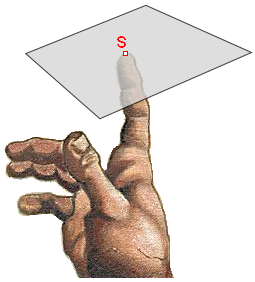
- gdy podeprzemy figurę w punkcie S,
utrzyma się ona w równowadze?
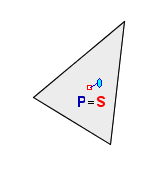
- gdy przypniemy figurę pinezką w punkcie S (P = S), nie będzie kołysania, to znaczy, że jeśli obrócimy figurę o dowolny kąt,
to utrzyma ona taką pozycję?
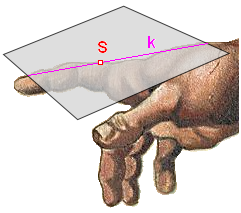
- gdy podeprzemy figurę dowolną prostą przechodzącą przez punkt S, utrzyma się ona w równowadze?
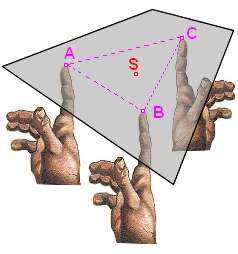
- gdy podeprzemy figurę w trzech punktach, to punkt S będzie leżał w obrębie trójkąta wyznaczonego przez te punkty?
- leży on (punkt S) na każdej prostej równowagi?
Środek ciężkości ma każdą z tych własności (tzn. na każde z powyższych pytań odpowiedź jest twierdząca). Można się o tym przekonać, eksperymentując.
A gdzie tu jest matematyka?
Teraz jeszcze nigdzie, ale może być. Już Archimedes zbudował teorię, w której wyznaczanie środka ciężkości sprowadził do czysto geometrycznych rozważań. Nie będziemy tu jej przytaczać (w szkole jej fragmenty ilustruje się rozważaniami o huśtawkach).
Powyższe pytania mogą prowokować, do stawiania następnych. Na przykład można się zastanawiać, jakie są zależności pomiędzy podanymi własnościami, tzn. czy z własności (X) wynika (Y). Ale może lepiej dać się sprowokować do... dalszych eksperymentów. Archimedes nim zbudował teorię, na pewno wcześniej znał z doświadczenia odpowiedzi na powyższe pytania. A Ty?
Drogi Czytelniku!
Jeśli dalej się wzbraniasz przed doświadczeniami, spróbuj przynajmniej pomedytować nad poniższymi pytaniami:
-- W trójkącie środkowe są prostymi równowagi. Środkowe dzielą trójkąt na dwa obszary o tym samym polu (czyli także o tej samej masie). Czy każda prosta równowagi dzieli pole figury (czyli także jej masę) na połowy?
-- Czy w każdej figurze jest tylko JEDEN środek ciężkości?
-- Czy w trapezie równoramiennym środek ciężkości leży w połowie wysokości leżącej w osi symetrii tego trapezu?
W tekście wykorzystano fragment dzieła M. A.
bez wiedzy i zgody autora. Przepraszamy.
Mamy nadzieję, że zostanie to nam wybaczone,
wszak dzieło użyte zostało w zbożnym celu.
Czy wiesz, kto z wrocławskich matematyków został uwiecz-niony na tym znakomitym portrecie w piżamie? Kto jest autorem tego obrazu? Gdzie można go obejrzeć?
Jako młody chłopak Knaster ożenił się z poznaną w Paryżu Marią Morską - muzą Skaman-drytów (zm. w 1945 roku). W czasach wrocła-wskich jego drugą żoną była Regina Lewandowska. Pierwszej żonie Knastera poświęcona jest książka Hanny Faryny-Paszkiewicz "Opium życia".
Steinhaus twierdził, że nazwisko Knaster brzmi w dopeł-niaczu Knastra, a sam Knaster upierał się przy formie Knastera. 
