Na szkielecie sześcianu po wyjęciu z mydlin powstaje piękna, kolorowa błona. Jest dość stabilna. Niestety niezbyt dobrze utrwala się na zdjęciu.

fot. Piotr Pawlikowski
Fizycy mówią, że jest to przykład powierzchni minimalnej. Napięcie powierzchniowe powoduje, że błona przyjmuje taki kształt, przy którym jej powierzchnia jest najmniejsza z możliwych.
Wygląda na to, że błona mydlana 'umie' rozwiązywać zadania optymalizacyjne (na znalezienie minimum). Komputer też 'umie' rozwiązywać takie zagadnienia (programem typu CAS przeznaczonym do obliczeń symbolicznych). Postanowiłem zatem obliczyć wymiary powierzchni minimalnej dla sześcianu.
Wyniki były zaskakujące!
Na zdjęciu widać, że badana powierzchnia wygląda jak klepsydra. Składa się z 13 ścian:
kwadratu (w środku), czterech trójkątów (opartych na krawędziach bocznych) i ośmiu trapezów (opartych na krawędziach podstaw).
Dzięki sterom 3D wielokąty w sześcianie można oglądać z różnych stron.
Górne są przezroczyste, aby nie zasłaniały reszty.
Niech krawędź sześcianu ma długość a = 1.
Pole P rozważanej powierzchni zależy tylko od x - długości boku środkowego kwadratu.
Łatwo je wyznaczyć (wskazówkę można zobaczyć na rysunku powyżej).
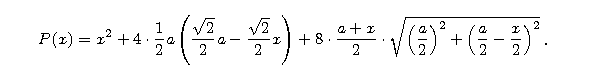
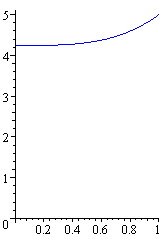 Aby znaleźć właściwe x, wystarczy narysować wykres tej funkcji
Aby znaleźć właściwe x, wystarczy narysować wykres tej funkcji
(przy a = 1) i odczytać, gdzie wykres ma 'dołek'.
To znaczy należy znaleźć takie x0, dla którego wartość funkcji P jest najmniejsza na przedziale (0, 1).
Przepis funkcji jest straszny, ale nie dla komputera.
Z wykresu widać, że... nie ma dołka!
Wygląda na to, że funkcja P na przedziale (0, 1) rośnie.
Ale
Można zmusić komputer, aby wyznaczył x0, a którym funkcja osiąga minimum.
W tym celu należy obliczyć pochodną funkcji P:
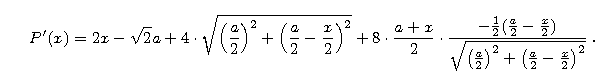
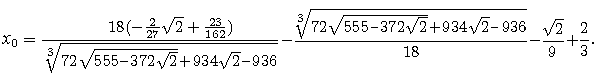
Na szczęście można zmusić komputer do podania jego przybliżenia:
x0 = 0,0729115569...
Z pozoru wszystko jest dobrze, ale proszę sprawdzić na zdjęciu, że
środkowy kwadrat w rzeczywistości jest radykalnie większy,
ma bok dużo dłuższy niż 7/100 długości krawędzi sześcianu!
Czy błona mydlana się myli? Czy otrzymana powierzchnia wcale nie ma minimalnego pola?
Popatrzmy na pewną modyfikację powyższej powierzchni.
Niech wszystkie trapezy z poprzedniego rysunku 'zegną się'.
Niech miejsce tych zgięć wyznacza punkt K leżący o y pod/nad środkiem odcinka AP.
Nowa powierzchnia składa się z:
- kwadratu o boku x,
- 16 trapezów,
- 4 pięciokątów.
Jej pole zależy od x i y.
Nieco trudniej je wyznaczyć (wskazówkę można zobaczyć na powyższym rysunku):
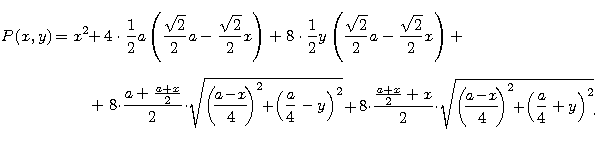
 Kolejny straszny wzór? Nie dla komputera.
Kolejny straszny wzór? Nie dla komputera.
Oczywiście
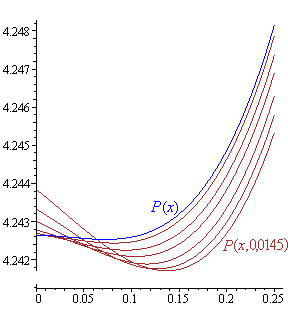
Zobaczmy kilka wykresów funkcji P (x, y)
dla ustalonych wartości y, na przykład:
P (x, 0,003),
P (x, 0,005),
P (x, 0,008),
P (x, 0,011),
P (x, 0,0145).
Te funkcje mają dołki niższe od dołka funkcji P(x) i leżące 'bardziej na prawo', czyli są bliższe temu, co widać na zdjęciu.
Uwaga. Tylko dla dorosłych
To oznacza, że zdjęcie się myli, albo że błędny jest nasz sposób jego odczytania!
Na zdjęciu nie ma kwadratu, 4 trójkątów i 8 trapezów!
Na zdjęciu nie ma też kwadratu, 4 pięciokątów i 16 trapezów!
Zegnijmy bowiem poprzednie trapezy tak, jak na rysunku poniżej
(środki odcinków AK i KP 'opadają' o z).
Teraz powierzchnia składa się z:
- kwadratu o boku x,
- 32 trapezów,
- 4 dziewięciokątów.
Jej pole zależy od x, y i z.
Trudno je wyznaczyć, ale od czego jest komputer! Otrzymamy:
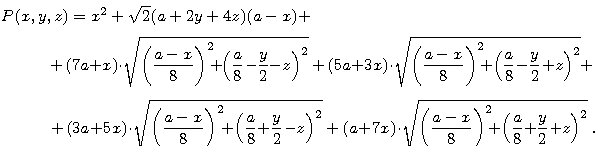
 Oczywiście:
Oczywiście:
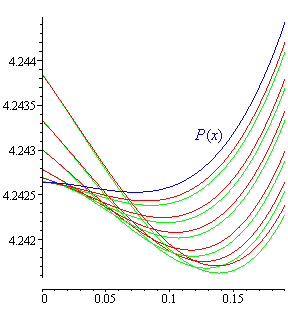
Zobaczmy kilka wykresów funkcji P (x, y, z)
dla ustalonych wartości y i z, na przykład:
P (x, 0,001), P (x, 0,001, 0,0005),
P (x, 0,003), P (x, 0,003, 0,0005),
P (x, 0,005), P (x, 0,005, 0,0005),
P (x, 0,008), P (x, 0,008, 0,0005),
P (x, 0,011), P (x, 0,011, 0,0005),
P (x, 0,0145), P (x, 0,0145, 0,0005).
Zielone minima są niższe od dołków czerwonych funkcji i leżą 'bardziej na prawo'.
A to właśnie oznacza, że na zdjęciu nie ma kwadratu, 4 pięciokątów i 16 trapezów!
A jak jest naprawdę?
Bardziej skomplikowanie. To, co widać na zdjęciu, to nie są wielokąty (w szczególności figura w środku nie jest kwadratem)! Ich kształty są tylko zbliżone do wielokątów.
Rzeczywistość czasami 'używa' bardziej skomplikowanych figur niż geometria.

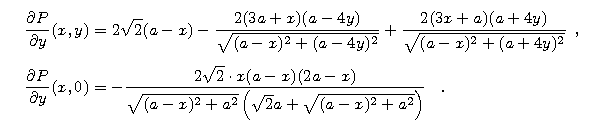 Ostatnia wielkość jest ujemna.
Ostatnia wielkość jest ujemna.


 To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.


